How did we get here? The story of algorithms.

Until recently, algorithms were a domain of computer scientists. Now, they have entered our lives and are pervasive. How did it happen?

Image by mehaniq41 (Adobe Stock Photos)

Until recently, algorithms were a domain of computer scientists. But now, they have entered our lives and are becoming pervasive. Algorithm is not a foreign word anymore. Algorithmic trading, algorithmic bias, the Facebook algorithm, even algorithmic warfare — all these terms have become part of our vocabulary in recent years. Some people go as far as claiming that we live in a new age: the age of the algorithm. But the algorithms are not that new. We have used them, knowingly or not, for hundreds and thousands of years. Algorithms are merely specific descriptions of step-by-step actions that need to happen to achieve a particular outcome[1]. They are one of the most common instruments of knowledge sharing.

Practically any process of teaching someone how to do something uses algorithms.

Some aspects of algorithms have changed in the last few decades though. In particular, the introduction of computers means that many algorithms today are dramatically more complex than we could have ever imagined in the past. How did the algorithms evolve to be so much more sophisticated today than they were in the past? Let’s have a brief look at their history.

Algorithms guiding human actions

A stamp issued September 6, 1983, in the Soviet Union, commemorating al-Khwārizmī’s (approximate) 1200th birthday; via Wikimedia Commons

The term algorithm derives from the name of Muhammad ibn Mūsā al’Khwārizmī, a ninth-century Persian mathematician. His latinized name, Algoritmi, meant “the decimal number system” and was used in this meaning for centuries. The modern notion of algorithm emerged in English in the nineteenth century[2], and became more commonly used since the 1950s, triggered by the emergence of first commercially available computers.

Long before algorithms got their modern name though, they were commonly created and used.

The first algorithms were captured on paper in Ancient Greece. Scholars such as Nicomachus of Gerasa or Euclid were then creating the building blocks of modern mathematics. To ease understanding and applicability of their ideas, they expressed many of them as step-by-step actions.

Nicomachus of Gerasa introduced the Sieve of Eratosthenes. The Sieve is used to this day by students learning to write efficient computer code. It helped simplify the process of identifying prime numbers. Prime numbers are natural numbers, greater than one, that cannot be formed by multiplying two smaller natural numbers. For instance, four is not a prime number because it can be formed by multiplying two by two. Five, in contrast, is a prime number, because no natural numbers, smaller than five, can be multiplied to form five. While it is not too hard to identify the first few prime numbers (for instance 2, 3, 5, 7, 11, 13, 17, 19, 23 and 29), finding large prime numbers takes a lot of time.[3] And large prime numbers are essential in cryptography. The Sieve of Eratosthenes gives step by step instructions for quickly removing all non-prime numbers from a defined set of numbers (for instance between 1 and 10,000) until only prime numbers are left. Today, there are numerous algorithms available, that simplify the task of identifying such numbers. The Sieve of Eratosthenes started a whole family of algorithms that have the same goal and are becoming better (quicker, or requiring fewer steps) at detecting prime numbers.

Sieve of Eratosthenes by SKopp at German Wikipedia [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0/)]

Euclid, the other scholar mentioned above, much better known than Nicomachus these days, introduced an algorithm for identifying the greatest common divisor of two numbers. Again, not always an easy task, but essential in many situations. Euclid’s algorithm helped to make this calculation easy. Why is Euclid’s algorithm helpful? Imagine you have a room with the exact size of 612 by 2006 centimeters that needs a new floor. Euclid’s algorithm will help you find the size of the largest square tiles that would neatly cover the floor. The answer, given by the algorithm, is 34 cm by 34 cm, resulting in a layout of 18 by 59 tiles. Of course, every tiler will tell you that the answer is wrong and that you have no idea what you’re doing because the algorithm doesn’t consider the grout width and leaves no space for it. Fear not: this can be calculated too, and neatly expressed as an algorithm.

Algorithms guiding machine actions

Over several hundred years that followed, many more algorithms were created and captured on paper. They were then used by individuals and followed step-by-step. The first algorithm meant to be executed on a machine was created by Ada Lovelace (née Byron) and published in 1843.

Ada Byron, aged four. Soon, she will become the world’s first computer programmer. By Artist: Alfred, Comte d’Orsay. Digital image; Somerville College, Oxford — Somerville College, Oxford, Public Domain, https://commons.wikimedia.org/w/index.php?curid=44246375

Ada was an intriguing character. She was born in 1815 as the only legitimate child of the poet Lord Byron. She developed great talents in mathematics. And since the love of poetry was clearly in her genes, she somehow managed to develop and balance both the love of science and poetry. Ada self-described her mindset as “poetical science”. As a skilled mathematician, she got to know Charles Babbage, who is often called “the father of computers,” thanks to his inventions. They both developed a working relationship and friendship. Ada was very interested in one of Charles’s designs — the Analytical Engine.

A diagram for the Analytical Engine. By ArnoldReinhold — Own work, CC BY 4.0, https://commons.wikimedia.org/w/index.php?curid=69497631

The Analytical Engine was a mechanical computer — a machine that automated computations. It was the Analytical Engine that she wrote the first algorithm for. Her work was a formula showing how to configure the Engine to calculate a particular complex sequence of numbers, called Bernoulli numbers. The formula is now widely recognized as the first computer algorithm in history.

Ada didn’t just limit herself to pure mathematical calculations. Given she lived in the nineteenth century, she was a true visionary.

While many of her contemporaries were seeing the first mechanical computers primarily as number-crunchers, she was asking what’s beyond performing calculations. She was curious about the broader potential of mechanical computers as collaborative tools. She was hoping to see computers that would empower humans much more than just through automating calculations.

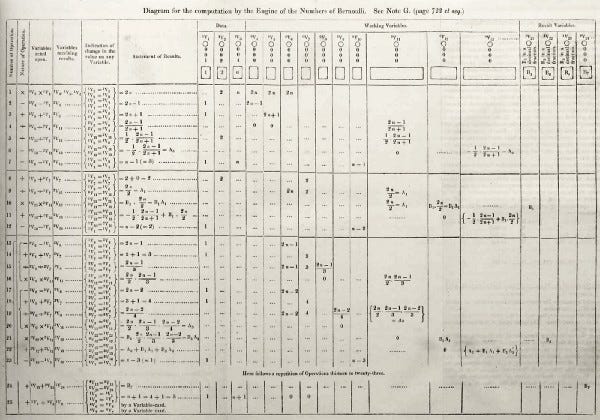
Lovelace’s diagram from “note G”, the first published computer algorithm, by Ada Lovelace — http://www.sophiararebooks.com/pictures/3544a.jpg, Public Domain, https://commons.wikimedia.org/w/index.php?curid=37285970

Unfortunately, the construction of the Analytical Engine was not completed before Ada’s death, and so she was never able to see her algorithm in action. Sadly, the Analytical Engine has not been built to this day. Another design of Charles Babbage, the Difference Engine №2, was built by the London Science Museum only in 1991. It was demonstrated to be functional, using materials and technologies available to Charles Babbage. It seems Babbage was just unlucky when it came to getting his designs built. Other partial implementations of Charles’s work exist elsewhere, but unfortunately, we cannot run Ada Byron’s algorithm on a real Analytical Engine.

The nineteenth-century became an era of “algorithms embedded in machines”.

There were plenty of them, automating all sorts of human actions. If you needed an intricate pattern on a piece of fabric, Joseph Marie Jacquard, a French weaver and merchant, had a solution for you: the Jacquard Loom. It allowed fabric manufacturers to produce sophisticated patterns using a series of perforated cards that instructed a loom how to weave. In a similar way, early telephone exchanges used sophisticated mechanical devices to connect phone calls. They automatically followed step by step instructions to ultimately get two people to talk to each other. These machines, whether looms or exchanges, were groundbreaking at their time, and are still impressive until this day. It is hard not to admire the levels of the intricacy of some of these machines. However, all these devices were still purely mechanical. They were made of levers, switches, shafts. They made a lot of noise. And they were very far from what we call computers these days.

Algorithms on general-purpose computers

It wasn’t until the 1930s when we saw the first mentions of algorithms in electronic (non-mechanical) computers. Alan Turing was among the first scientists who formally captured how individuals performed computations. Turing’s goal was to capture a general process, rather than one specific to a particular task such as for identifying prime numbers or calculating the greatest common divisor. The general process could then be used to perform specific tasks. Turing’s conceptual work led to the development of what is now known as the Turing Machine. The Turing Machine, in turn, led to the emergence of general purpose computers. The general purpose prefix is essential here. Contrary to previous machines, the new computers would execute arbitrary sets of instructions. They could be used for purposes not even predicted by their creators. In other words: Turing’s work led to the development of computers on which we can install and run applications.

No Flappy Bird on your smartphone without the concept of a Turing machine.

Decades later, algorithms have become extremely sophisticated. So sophisticated, in fact, that we often find it impossible to explain how they work. In the twentieth century many preferred to think about computer algorithms as black boxes. You didn’t have to understand how exactly they worked. All you cared about were the inputs — what went into the black box — and outputs — what came out. This simplification was a choice. In the twenty-first century, for some algorithms, this is not a choice anymore: humans cannot explain exactly how algorithms reach particular outputs, and so we are forced to think about these algorithms as black, or perhaps magical, boxes. One group of such algorithms are some of the artificial intelligence algorithms. We can explain their principles. For instance, we can say that an algorithm uses an artificial neural network. We can also explain how the network was created, and how the input resulted with a particular output. What we cannot explain, however, is why this particular result was the output of the algorithm, beyond a pure mechanical explanation. Eric L. Loomis, whose length of incarceration depended on an algorithm, tried to understand why the COMPAS algorithm assessed him as a high risk criminal. It was simply impossible. The sophistication of algorithms is often overwhelming. And this is just the beginning.

We live in a world where algorithms are everywhere — not just on paper or in our minds, but controlling machines, computers and robots.

They are small, ubiquitous, and — at least in some cases — inexplicable.

[1] A more formal definition of an algorithm is “an unambiguous specification of how to solve a class of problems” or “a self-contained step-by-step set of operations to be performed” [source: Wikipedia Algorithm]

[2] www.oed.com/view/Entry/4959

[3] As of October 2018, the largest known prime number is 277,232,917− 1, a number with 23,249,425 digits. Just checking whether this single number is prime took six days of non-stop computing on a contemporary home computer. (https://www.mersenne.org/primes/press/M77232917.html)